享元模式

UML
Java
Scheme

享元模式的主要目的是实现对象的共享，即共享池，当系统中对象多的时候可以减少内存的开销，通常与工厂模式一起使用

UML

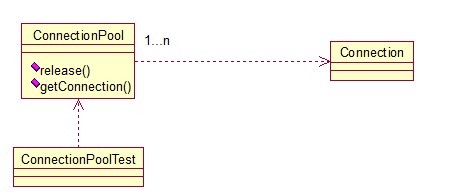
Java

对于数据库连接池，url、driverClassName、username、password及dbname，这些属性对于每个连接来说都是一样的，所以就适合用享元模式来处理，建一个工厂类，将上述类似属性作为内部数据，其它的作为外部数据，在方法调用时，当做参数传进来，这样就节省了空间，减少了实例的数量：

public class ConnectionPool {
    private Vector<Connection> pool;

    /*公有属性*/
    private String url = "jdbc:mysql://localhost:3306/test";
    private String username = "root";
    private String password = "root";
    private String driverClassName = "com.mysql.jdbc.Driver";

    private int poolSize = 100;
    private static ConnectionPool instance = null;
    Connection conn = null;

    /*构造方法，做一些初始化工作*/
    private ConnectionPool() {
        pool = new Vector<Connection>(poolSize);

        for (int i = 0; i < poolSize; i++) {
            try {
                Class.forName(driverClassName);
                conn = DriverManager.getConnection(url, username, password);
                pool.add(conn);
            } catch (ClassNotFoundException e) {
                e.printStackTrace();
            } catch (SQLException e) {
                e.printStackTrace();
            }
        }
    }

    /* 返回连接到连接池 */
    public synchronized void release() {
        pool.add(conn);
    }

    /* 返回连接池中的一个数据库连接 */
    public synchronized Connection getConnection() {
        if (pool.size() > 0) {
            Connection conn = pool.get(0);
            pool.remove(conn);
            return conn;
        } else {
            return null;
        }
    }
}

Scheme

lazy evalatuion：使用delay来保存计算结果的表达式(promise)，而使用force来返回对应的计算结果，这样可以不但能计算无穷的结果，还能有效避免内存中大量的无效计算结果

定义各种lazy操作：car, cdr, cons, map, filter, ref, head

;; car for lazy evaluation
(define lazy-car car)

;; cdr for lazy evaluation
(define (lazy-cdr ls)
  (force (cdr ls)))

;; lazy cons
(define-syntax lazy-cons
  (syntax-rules ()
    ((_ a b) (cons a (delay b)))))

;; lazy map
(define (lazy-map fn . lss)
  (if (memq '() lss)
      '()
      (lazy-cons (apply fn (map lazy-car lss))
                 (apply lazy-map fn (map lazy-cdr lss)))))

;; lazy filter
(define (lazy-filter pred ls)
  (if (null? ls)
      '()
      (let ((obj (lazy-car ls)))
        (if (pred obj)
            (lazy-cons obj  (lazy-filter pred (lazy-cdr ls)))
            (lazy-filter pred (lazy-cdr ls))))))

;; returns n-th item of the lazy list
(define (lazy-ref ls n)
  (if (= n 0)
      (lazy-car ls)
      (lazy-ref (lazy-cdr ls) (- n 1))))

;; returns first n items of the ls
(define (head ls n)
  (if (= n 0)
      '()
      (cons (lazy-car ls) (head (lazy-cdr ls) (- n 1)))))

定义两个无穷数列：

     ;;;;  sequences

    ;;; infinite sequences represented by a_(n+1) = f(a_n)
(define (inf-seq a0 f)
  (lazy-cons a0 (inf-seq (f a0) f)))

    ;;; 等差数列
(define (ari a0 d)
  (inf-seq a0 (lambda (x) (+ x d))))

    ;;; 等比数列
(define (geo a0 r)
  (inf-seq a0 (lambda (x) (* x r))))

测试：

(define g1 (geo 1 2))
;;Value: g1

(define g2 (geo 1 (/ 1 2)))
;;Value: g2

(head g1 10)
;;Value 12: (1 2 4 8 16 32 64 128 256 512)

(head g2 10)
;;Value 13: (1 1/2 1/4 1/8 1/16 1/32 1/64 1/128 1/256 1/512)

(head (lazy-map * g1 g2) 10)
;;Value 14: (1 1 1 1 1 1 1 1 1 1)

(define ar1 (ari 1 1))
;;Value: ar1

(head ar1 10)
;;Value 15: (1 2 3 4 5 6 7 8 9 10)

(head (lazy-filter even? ar1) 10)
;;Value 16: (2 4 6 8 10 12 14 16 18 20)

Previous：桥接模式

Home：目录

享元模式

Table of Contents

UML

Java

Scheme