改善算法
Table of Contents
接下来将学习优化算法,这能让神经网络运行得更快
机器学习的应用是一个高度依赖经验的过程,伴随着大量迭代的过程,需要训练诸多模型,才能找到合适的那一个,所以,优化算法能够帮助快速训练模型 其中一个难点在于,深度学习不能在没有大数据领域发挥最大的效果,而在巨大的数据集基础上进行训练速度很慢。因此,会发现,使用快速的优化算法能够大大提高效率
Mini-batch 梯度下降
首先来谈谈 mini-batch 梯度下降法

向量化能够有效地对所有个样本进行计算,允许处理整个训练集,而无需某个明确的公式。所以要把训练样本放入巨大的矩阵 \(X\) 当中去, \(X=[x^{(1)} x^{(2)} x^{(3)} \ldots x^{(m)}]\) ,\(Y\) 也是如此,\(Y=[y^{(1)} y^{(2)} y^{(3)} \ldots y^{(m)}]\) ,所以 \(X\) 的维数是 \((n_x, m)\) , \(Y\) 的维数是 \((1, m)\) ,向量化能够相对较快地处理 \(m\) 所有个样本
如果m 很大的话,处理速度仍然缓慢。比如说,如果 m 是500万或5000万或者更大的一个数 在对整个训练集执行梯度下降法时,要做的是,必须处理整个训练集,然后才能进行一步梯度下降法 然后需要再重新处理500万个训练样本,才能进行下一步梯度下降法 所以如果在处理完整个500万个样本的训练集之前,先让梯度下降法处理一部分,算法速度会更快
可以把训练集分割为小一点的子集训练,这些子集被取名为 mini-batch ,假设每一个子集中只有1000个样本,那么把其中的 \(x^{(1)}\) 到 \(x^{(1000)}\) 取出来,将其称为第一个子训练集,然后再取出接下来的1000个样本,从 \(x^{(1001)}\) 到 \(x^{(2000)}\) ,然后再取1000个样本,以此类推。
- 把 \(x^{(1)}\) 到 \(x^{(1000)}\) 称为 \(X^{\{1\}}\)
- 把 \(x^{(1001)}\) 到 \(x^{(2000)}\) 称为 \(X^{\{2\}}\)
- 如果训练样本一共有500万个,每个mini-batch都有1000个样本,也就是说,有5000个mini-batch,因为5000乘以1000就是500万,所以最后得到的就是 \(X^{\{5000\}}\)
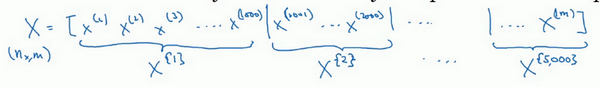
对 \(Y\) 也要进行相同处理,相应地拆分 \(Y\) 的训练集,所以这是 \(Y^{\{1\}}\) ,然后从 \(y^{(1001)}\) 到 \(y^{(2000)}\) ,这个叫 \(Y^{\{2\}}\) ,一直到 \(Y^{\{5000\}}\)

mini-batch的数量 \(t\) 组成了\(X^{\{t\}}\) 和 \(Y^{\{t\}}\) ,这就是1000个训练样本,包含相应的输入输出对
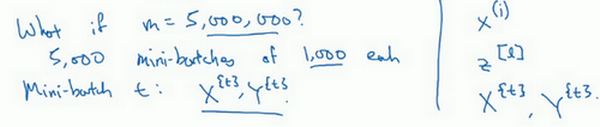
之前使用了上角小括号 \((i)\) 表示训练集里的值,所以 \(x^{(i)}\) 是第 \(i\) 个训练样本。用了上角中括号 \([l]\) 来表示神经网络的层数,\(z^{[l]}\) 表示神经网络中第 \(l\) 层的 \(z\) 值,现在引入了大括号 \(t\) 来代表不同的mini-batch,所以有 \(X^{\{t\}}\) 和 \(Y^{\{t\}}\)
batch梯度下降法指的是之前讲过的梯度下降法算法,就是同时处理整个训练集 这个名字就是来源于能够同时看到整个batch训练集的样本被处理 相比之下,mini-batch梯度下降法,指的是每次同时处理的单个的 mini-batch , 而不是同时处理全部的 X 和 Y 训练集 那么究竟mini-batch梯度下降法的原理是什么?
在训练集上运行mini-batch梯度下降法,运行 \(for \quad t = 1 \ldots 5000\) ,因为有5000个各有1000个样本的组,在for循环里要做得基本就是对 \(X^{\{t\}}\) 和 \(Y^{\{t\}}\) 执行一步梯度下降法