Table of Contents
>#+TITLE: 循环序列模型
为什么选择序列模型?
接下来将学会序列模型,它是深度学习中最令人激动的内容之一
循环神经网络 RNN 之类的模型在语音识别、自然语言处理和其他领域中引起变革。先看一些例子,这些例子都有效使用了序列模型:
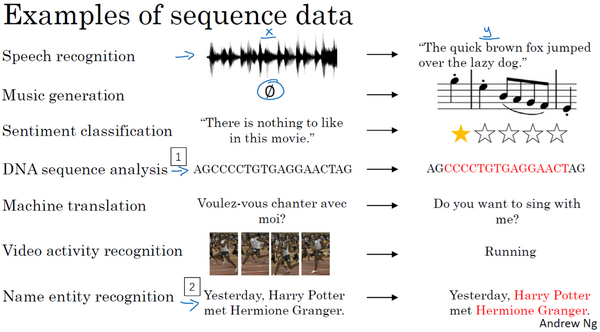
在进行 语音识别 时,给定了一个输入音频片段 \(X\) ,并要求输出对应的文字记录 \(Y\) 。这个例子里输入和输出数据都是序列模型,因为\(X\) 是一个按时播放的音频片段,输出\(Y\) 是一系列单词
之后将要学到的一些序列模型,如循环神经网络等等在语音识别方面是非常有用的
- 音乐生成 问题是使用序列数据的另一个例子,在这个例子中,只有输出数据 \(Y\) 是序列,而输入数据可以是空集,也可以是个单一的整数,这个数可能指代想要生成的音乐风格,也可能是想要生成的那首曲子的头几个音符。输入的\(X\) 可以是空的,或者就是个数字,然后输出序列\(Y\)
在处理 情感分类 时,输入数据 \(X\) 是序列
类似这样的输入:“There is nothing to like in this movie.”, 你认为这句评论对应几星?
序列模型在 DNA序列分析 中也十分有用
DNA可以用A、C、G、T四个字母来表示 给定一段DNA序列,能够标记出哪部分是匹配某种蛋白质的吗?
在 机器翻译 过程中
会得到这样的输入句:“Voulez-vou chante avecmoi?”(法语:要和我一起唱么?) 然后要求你输出另一种语言的翻译结果
- 在进行 视频行为识别 时,可能会得到一系列视频帧,然后要求你识别其中的行为
- 在进行 命名实体识别 时,可能会给定一个句子要你识别出句中的人名
所有这些问题都可以被称作使用 标签数据 \((X, Y)\) 作为训练集的监督学习。但从这一系列例子中可以看出序列问题有很多不同类型。有些问题里,输入数据 \(X\) 和输出数据 \(Y\) 都是序列,但就算在那种情况下,\(X\) 和 \(Y\) 有时也会不一样长。或者像上图编号1所示和上图编号2的 \(X\) 和 \(Y\) 有相同的数据长度。在另一些问题里,只有 \(X\) 或者只有 \(Y\) 是序列
数学符号
比如说想要建立一个序列模型,它的输入语句是这样的:“Harry Potter and Herminoe Granger invented a new spell.” 这些人名都是出自于J.K.Rowling笔下的系列小说Harry Potter 这就是一个命名实体识别问题,这常用于搜索引擎 比如说索引过去24小时内所有新闻报道提及的人名,用这种方式就能够恰当地进行索引 命名实体识别系统可以用来查找不同类型的文本中的人名、公司名、时间、地点、国家名和货币名等等

现在给定这样的输入数据 \(x\) ,假如想要一个序列模型输出 \(y\) ,使得输入的每个单词都对应一个输出值,同时这个 \(y\) 能够表明输入的单词是否是人名的一部分
技术上来说这也许不是最好的输出形式,还有更加复杂的输出形式 它不仅能够表明输入词是否是人名的一部分,它还能够告诉你这个人名在这个句子里从哪里开始到哪里结束 比如Harry Potter(上图编号1所示)、Hermione Granger(上图标号2所示)
这个输入数据是9个单词组成的序列,所以最终会有9个特征集和来表示这9个单词,并按序列中的位置进行索引 \(x^{<1>}\) , \(x^{<2>}\) , \(x^{<3>}\) 等等一直到 \(x^{<9>}\) 来索引不同的位置,将用 \(x^{<\text{t}>}\) 来索引这个序列的中间位置。意味着它们是时序序列,但不论是否是时序序列,都将用 \(t\) 来索引序列中的位置
输出数据也是一样,还是用 \(y^{<1>}\) , \(y^{<2>}\) , \(y^{<3>}\) 等等一直到 \(y^{<9>}\) 来表示输出数据。同时 \(T_x\) 用来表示输入序列的 长度 ,这个例子中输入是9个单词,所以 \(T_x = 9\) 。\(T_y\) 用来表示输出序列的长度。在这个例子里 \(T_x = T_y\) ,当然两者可以有不同的值
之前 \(x^{(i)}\) 用来表示第 \(i\) 个训练样本,所以为了指代第 \(t\) 个元素,或者说是训练样本 \(i\) 的序列中第 \(t\) 个元素用 \(x^{(i)<\text{t}>}\) 这个符号来表示。如果 \(T_x\) 是序列长度,那么训练集里不同的训练样本就会有不同的长度,所以 \(T_x^{(i)}\) 就代表第 \(i\) 个训练样本的输入序列长度。同样 \(y^{(i)<\text{t}>}\) 代表第 \(i\) 个训练样本中第 \(t\) 个元素, \(T_y^{(i)}\) 就是第 \(i\) 个训练样本的输出序列的长度 。在这个例子中, \(T_x^{(i)} = 9\) ,但如果另一个样本是由15个单词组成的句子,那么对于这个训练样本 \(T_x^{(i)} = 15\)
词典
既然这个例子是NLP,也就是自然语言处理,这是初次涉足自然语言处理
一件需要事先决定的事是怎样表示一个序列里单独的单词,你会怎样表示像Harry这样的单词,实际 x^{<1>} 应该是什么?
想要表示一个句子里的单词,第一件事是做一张词表,有时也称为词典,意思是列一列表示方法中用到的单词。这个词表(下图所示)中的第一个词是 a ,也就是说词典中的第一个单词是a,第二个单词是 Aaron ,然后更下面一些是单词 and ,再后面会找到 Harry ,然后找到 Potter ,这样一直到最后,词典里最后一个单词可能是 Zulu
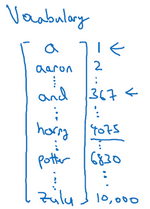
因此a是第 1 个单词, Aaron是第 2 个单词,在这个词典里,and出现在 367 这个位置上,Harry是在 4075 这个位置,Potter在 6830 ,词典里的最后一个单词Zulu可能是第 10,000 个单词。所以在这个例子中用了10,000个单词大小的词典,这对现代自然语言处理应用来说太小了
对于商业应用来说,或者对于一般规模的商业应用来说30,000到50,000词大小的词典比较常见,但是100,000词的也不是没有 有些大型互联网公司会用百万词,甚至更大的词典 不过这里将用10,000词大小的词典做说明,因为这是一个很好用的整数
如果选定了10,000词的词典,构建这个词典的一个方法是遍历训练集,并且找到前10,000个常用词,也可以去浏览一些网络词典,它能告诉你英语里最常用的10,000个单词,接下来可以用 one-hot 表示法来表示词典里的每个单词
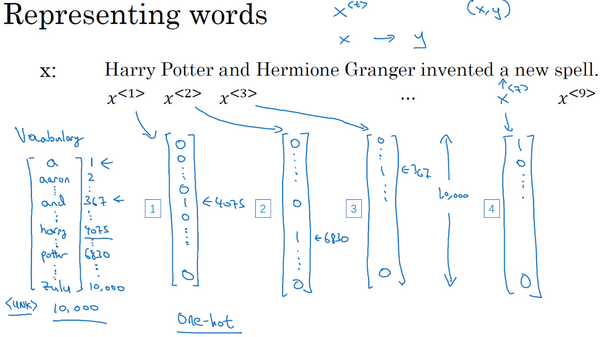
- 在这里 \(x^{<1>}\) 表示 Harry 这个单词,它就是一个第 4075 行是1,其余值都是0的向量(上图编号1所示),因为那是Harry在这个词典里的位置
- 同样 \(x^{<2>}\) 是个第 6830行 是1,其余位置都是0的向量(上图编号2所示)
- and在词典里排第367,所以 \(x^{<3>}\) 就是第 367行 是1,其余值都是0的向量(上图编号3所示)
- 因为a是字典第一个单词,\(x^{<7>}\) 对应a,那么这个向量的第 1 个位置为1,其余位置都是0的向量(上图编号4所示)
如果词典大小是10,000的话,那么这里的每个向量都是10,000维的
所以这种表示方法中, \(x^{<\text{t}>}\) 指代句子里的任意词,它就是个 one-hot 向量,因为它只有一个值是1,其余值都是0,所以会有9个one-hot向量来表示这个句中的9个单词。这样就能在序列模型 \(X\) 和目标输出 \(Y\) 之间学习建立一个映射。可以把它当作监督学习的问题,给定带有 \((x, y)\) 的标签的数据
如果遇到了一个不在词表中的单词? 答案就是创建一个新的标记,也就是一个叫做Unknow Word的伪造单词,用<UNK>作为标记,来表示不在词表中的单词
循环神经网络模型
可以尝试的方法之一是使用标准神经网络,在之前的例子中,有9个输入单词。想象一下,把这9个输入单词,可能是9个one-hot向量,然后将它们输入到一个标准神经网络中,经过一些隐藏层,最终会输出9个值为0或1的项,它表明每个输入单词是否是人名的一部分
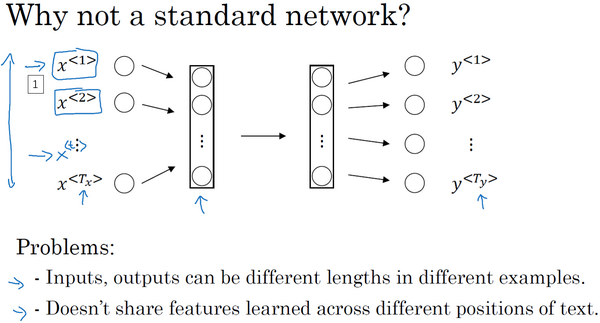
但结果表明这个方法并不好,主要有几个问题:
是输入和输出数据在不同例子中可以有不同的长度,不是所有的例子都有着同样输入长度 \(T_x\) 或是同样输出长度 \(T_y\) 的
即使每个句子都有最大长度,也许你能够填充 或 零填充 使每个输入语句都达到最大长度 但仍然看起来不是一个好的表达方式
一个像这样单纯的神经网络结构,它并不共享从文本的不同位置上学到的特征。具体来说,如果神经网络已经学习到了在位置1出现的Harry可能是人名的一部分,那么如果Harry出现在其他位置,比如 \(x^{<\text{t}>}\) 时,它也能够自动识别其为人名的一部分的话,这就很棒了
这可能类似于在卷积神经网络中看到的,希望将部分图片里学到的内容快速推广到图片的其他部分
之前提到过这些 \(x^{<1>}\) , \(x^{<2>}\) 都是10,000维的one-hot向量,因此这会是十分庞大的输入层。如果总的输入大小是最大单词数乘以10,000,那么第一层的权重矩阵就会有着巨量的参数。但循环神经网络就没有上述的两个问题
和在卷积网络中学到的类似,用一个更好的表达方式也能够让你减少模型中参数的数量
那么什么是循环神经网络呢?
先建立一个(下图编号1所示)。如果以从左到右的顺序读这个句子,第一个单词就是,假如说是 \(x^{<1>}\) :
- 将第一个词输入一个神经网络层(第一个神经网络的隐藏层) 可以让神经网络尝试预测输出,判断这是否是人名的一部分
- 循环神经网络做的是,当它读到句中的第二个单词时,假设是 \(x^{<2>}\) ,它不是仅用 \(x^{<2>}\) 就预测出 \(\hat{y}^{<2>}\) ,他也会输入一些来自时间步1的信息
- 具体而言,时间步1的激活值就会传递到时间步2
- 然后,在下一个时间步,循环神经网络输入了单词 \(x^{<3>}\) ,然后它尝试预测输出了预测结果 \(\hat{y}^{<3>}\) ,等等
- 一直到最后一个时间步,输入了 \(x^{<\mathbf{T}_{x}>}\) ,然后输出了 \(\hat{y}^{<\mathbf{T}_{y}>}\)
至少在这个例子中 \(T_x = T_y\) ,如果 \(T_x\) 和 \(T_y\) 不相同,这个结构会需要作出一些改变。总之在每一个时间步中,循环神经网络传递一个激活值到下一个时间步中用于计算
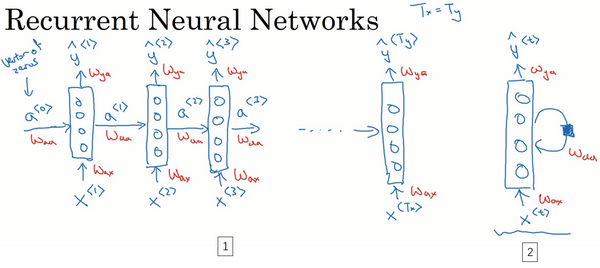
整个流程,在零时刻需要构造一个激活值 \(a^{<0>}\) ,这通常是 零向量
有些研究人员会随机用其他方法初始化,不过使用零向量作为零时刻的伪激活值是最常见的选择
在一些研究论文中或是一些书中会看到这类神经网络,用这样的图形来表示(上图编号2所示),在每一个时间步中,输入 \(x^{<\text{t}>}\) 然后输出 \(y^{<\text{t}>}\) 。为了表示循环连接有时会画个 圈 ,表示 输回网络层 ,同样会画一个 黑色方块 ,来表示在这个黑色方块处会 延迟 一个时间步
我个人认为这些循环图很难理解,更倾向于使用左边这种分布画法(上图编号1所示) 不过如果在教材中或是研究论文中看到了右边这种图表的画法(上图编号2所示),它可以在心中将这图展开成左图那样
参数
循环神经网络是从左向右扫描数据,同时每个时间步的参数也是共享的
用 \(W_{ax}\) 来表示管理着从 \(x^{<1>}\) 到隐藏层的连接的一系列参数,每个时间步使用的都是相同的参数 \(W_{ax}\) 。而激活值也就是水平联系是由参数 \(W_{aa}\) 决定的,同时每一个时间步都使用相同的参数 \(W_{aa}\) ,同样的输出结果由 \(W_{ya}\) 决定。下图详细讲述这些参数是如何起作用:
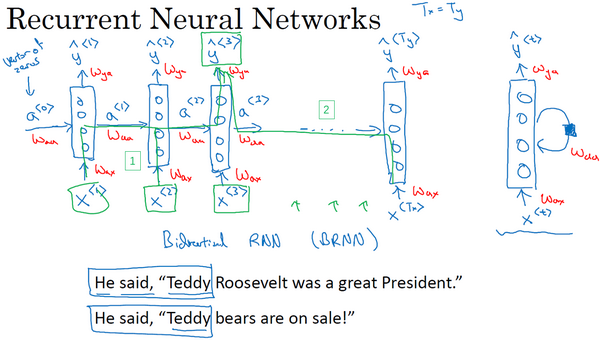
在这个循环神经网络中,在预测时,不仅要使用 \(x^{<3>}\) 的信息,还要使用来自 \(x^{<1>}\) 和 \(x^{<2>}\) 的信息,因为来自 \(x^{<1>}\) 的信息可以通过这样的路径(上图编号1所示的路径)来帮助预测。这个循环神经网络的一个缺点就是它只使用了这个序列中之前的信息来做出预测,尤其当预测时,它没有用到 \(x^{<4>}\) , \(x^{<5>}\) ,等等的信息
所以这就有一个问题,因为如果给定了这个句子,“Teddy Roosevelt was a great President.” 为了判断Teddy是否是人名的一部分,仅仅知道句中前两个词是完全不够的,还需要知道句中后部分的信息,这也是十分有用的 因为句子也可能是这样的,“Teddy bears are on sale!” 因此如果只给定前三个单词,是不可能确切地知道Teddy是否是人名的一部分 第一个例子是人名,第二个例子就不是,所以不可能只看前三个单词就能分辨出其中的区别
这样特定的神经网络结构的一个限制是 它在某一时刻的预测仅使用了从序列之前的输入信息并没有使用序列中后部分的信息
我们会在之后的双向循环神经网络(BRNN)的视频中处理这个问题 但对于现在,这个更简单的单向神经网络结构就够来解释关键概念了 之后只要在此基础上作出修改就能同时使用序列中前面和后面的信息来预测 不过会在之后讲述这些内容,接下来具体地写出这个神经网络计算了些什么
向前传播
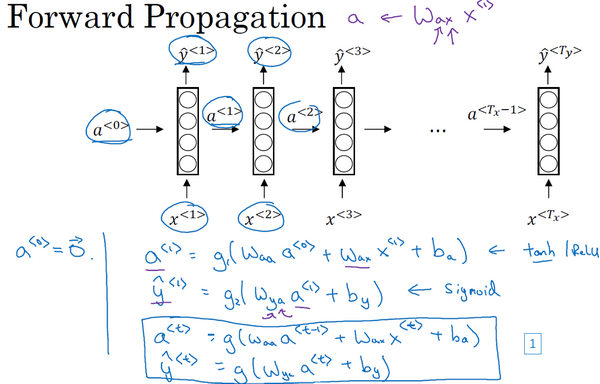
这里是一张清理后的神经网络示意图,一般开始先输入 \(a^<0>\) ,它是一个零向量。接着就是前向传播过程,先计算激活值 \(a^{<1>}\) ,然后再计算 \(y^{<1>}\)
\begin{equation} a^{<1>} = g_1(W_{aa}a^{<0>} + W_{ax}x^{<1>} + b_a) \\ \hat{y}^{<1>} = g_2(W_{ya}a^{<1>} + b_y) \end{equation}用这样的符号约定来表示这些矩阵下标,举个例子 \(W_{ax}\) ,第二个下标 \(x\) 意味着 \(W_{ax}\) 要乘以某个 \(x\) 类型的量,然后第一个下标 \(a\) 表示它是用来计算某个 \(a\) 类型的变量。同样的,可以看出这里的 \(W_{ya}\) 乘上了某个 \(a\) 类型的量,用来计算出某个 \(y\) 类型的量
循环神经网络用的激活函数经常是 \(tanh\) ,不过有时候也会用 \(ReLU\) ,但是 \(tanh\) 是更通常的选择
有其他方法来避免梯度消失问题,将在之后进行讲述
选用哪个激活函数是取决于输出:
- 如果它是一个二分问题,那么会用 \(sigmoid\) 函数作为激活函数
- 如果是类别分类问题的话,那么可以选用 \(softmax\) 作为激活函数
对于命名实体识别来说只可能是0或者1,那这里第二个激活函数可以是sigmoid激活函数
更一般的情况下,在 \(t\) 时刻:
\begin{equation} a^{<\text{t}>} = g_1(W_{aa}a^{<\text{t}-1>} + W_{ax}x^{<\text{t}>} + b_a) \\ \hat{y}^{<\text{t}>} = g_2(W_{ya}a^{<\text{t}>} + b_y) \end{equation}这些等式定义了神经网络的前向传播,可以从零向量 \(a^<0>\) 开始,然后用 \(a^{<0>}\) 和 \(x^{<1>}\) 来计算出 \(a^{<1>}\) 和 \(\hat{y}^<1>\) ,然后用 \(x^{<2>}\) 和 \(a^{<1>}\) 一起算出 \(a^{<2>}\) 和 \(\hat{y}^{<2>}\) 等等,像图中这样,从左到右完成前向传播
现在为了建立更复杂的神经网络,要将这个符号简化一下
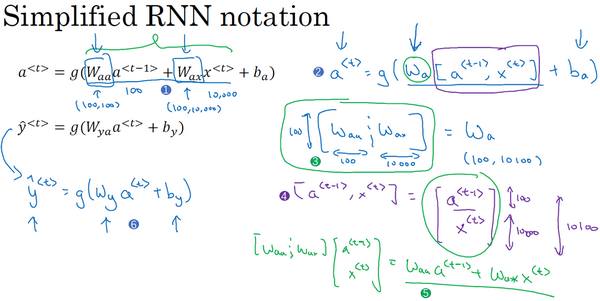
将这部分 \(a^{<\text{t}>} = g_1(W_{aa}a^{<\text{t}-1>} + W_{ax}x^{<\text{t}>} + b_a\) (上图编号1所示)以更简单的形式写作 \(a^{<\text{t}>} = g(W_a[a^{<\text{t}-1>}, x^{<\text{t}>}] + b_a\) (上图编号2所示),那么左右两边划线部分应该是等价的:
定义 \(W_a\) 的方式是将矩阵 \(W_{aa}\) 和矩阵 \(W_{ax}\) 水平并列放置, \([W_{aa} \vdots W_{ax}] = W_a\) (上图编号3所示)
举个例子,如果 a 是100维的,然后延续之前的例子,x 是10,000维的 那么 W_aa 就是个 (100, 100) 维的矩阵,W_ax 就是个(100, 10000)维的矩阵 因此如果将这两个矩阵堆起来,W_a 就会是个(100, 10100) 维的矩阵
- 符号 \([a^{\text{t}-1}, x^{\text{t}}]\) 的意思是将这两个向量吹着堆在一起,,即 \begin{bmatrix} a^{\text{t}-1} \\ x^{\text{t}} \end{bmatrix} (上图编号4所示),最终这就是个 10100维的向量
可以自己检查一下,用这个矩阵乘以这个向量,刚好能够得到原来的量,因为此时:
\begin{equation} \begin{bmatrix} W_{aa} & \vdots & W_{ax} \end{bmatrix} \ast \begin{bmatrix} a^{\text{t}-1} \\ x^{\text{t}} \end{bmatrix} = W_{aa}a^{<\text{t}-1>} + W_{ax}x^{<\text{t}>} \end{equation}
这种记法的好处是可以不使用两个参数矩阵和,而是将其压缩成一个参数矩阵 所以当建立更复杂模型时这就能够简化要用到的符号
同样对于这个例子 \(\hat{y}^{<\text{t}>} = g_2(W_{ya}a^{<\text{t}>} + b_y)\) ,会用更简单的方式重写 \(\hat{y}^{<\text{t}>} = g(W_ya^{<\text{t}>} + b_y)\) (上图编号6所示)。现在 \(W_y\) 和符号 \(b_y\) 仅有一个下标,它表示在计算时会输出什么类型的量,所以 \(W_y\) 就表明它是计算 \(y\) 类型的量的权重矩阵,而上面的 \(W_a\) 和 \(b_a\) 则表示这些参数是用来计算 \(a\) 类型或者说是激活值的
RNN前向传播示意图:
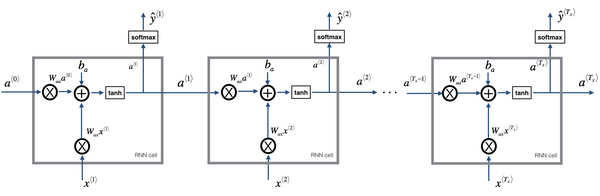
向后传播
和之前一样,在编程框架中实现循环神经网络时,编程框架通常会自动处理反向传播 但在循环神经网络中,对反向传播的运行有一个粗略的认识还是非常有用的
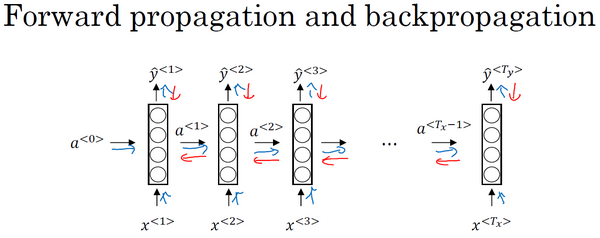
已经见过对于前向传播(上图蓝色箭头所指方向)怎样在神经网络中从左到右地计算这些激活项,直到输出所有地预测结果。而对于反向传播,反向传播地计算方向(上图红色箭头所指方向)与前向传播基本上是相反的
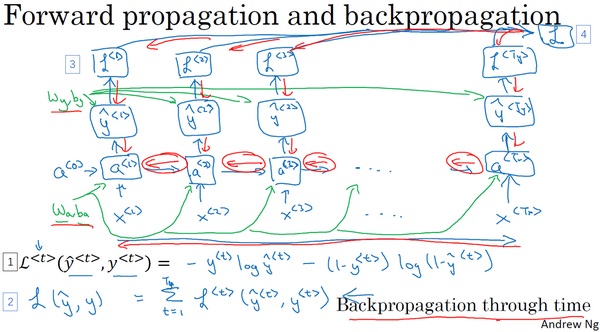
为了计算反向传播,还需要一个损失函数。先定义一个元素损失函数(上图编号1所示)
\begin{equation} L^{<\text{t}>}(\hat{y}^{<\text{t}>}, y^{<\text{t}>}) = -y^{<\text{t}>}\log{\hat{y}^{<\text{t}>}} - (1-y^{<\text{t}>})\log{1-\hat{y}^{<\text{t}>}} \end{equation}它对应的是序列中一个具体的词,如果它是某个人的名字,那么 \(y^{<\text{t}>}\) 的值就是1,然后神经网络将输出这个词是名字的概率值,比如0.1。将它定义为标准逻辑回归损失函数,也叫 交叉熵 损失函数 Cross Entropy Loss
它和之前在二分类问题中看到的公式很像 所以这是关于单个位置上或者说某个时间步上某个单词的预测值的损失函数
现在我们来定义整个序列的损失函数,将 \(\mathbf{J}\) 定义为(上图编号2所示)
\begin{equation} \mathbf{J}(\hat{y}, y) = \sum_{t=1}^{\mathbf{T}_x}L^{<\text{t}>}(\hat{y}^{<\text{t}>}, y^{<\text{t}>}) \end{equation}在这个计算图中:
- 通过 \(y^{<1>}\) 可以计算对应的损失函数,于是计算出第一个时间步的损失函数(上图编号3所示)
- 然后计算出第二个时间步的损失函数
- 然后是第三个时间步
- 一直到最后一个时间步
- 最后为了计算出总体损失函数,要把它们都加起来,通过下面的等式(上图编号2所示的等式)计算出最后的(上图编号4所示),也就是把每个单独时间步的损失函数都加起来
在之前的例子中,已经见过反向传播,所以应该能够想得到反向传播算法需要在相反的方向上进行计算和传递信息 最终做的就是把前向传播的箭头都反过来,在这之后你就可以计算出所有合适的量,然后就可以通过导数相关的参数,用梯度下降法来更新参数
在这个反向传播的过程中,最重要的信息传递或者说最重要的递归运算就是这个 从右到左 的运算,这也就是为什么这个算法有一个很别致的名字,叫做 通过(穿越)时间反向传播 backpropagation through time
取这个名字的原因是对于前向传播,需要从左到右进行计算,在这个过程中,时刻不断增加 而对于反向传播,需要从右到左进行计算,就像时间倒流 “通过时间反向传播”,就像穿越时光,这种说法听起来就像是需要一台时光机来实现这个算法一样
RNN反向传播示意图:
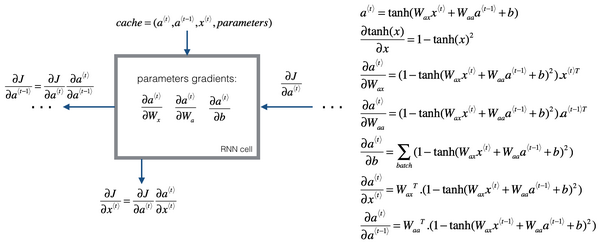
到目前为止,只见到了RNN中一个主要的例子,其中输入序列的长度和输出序列的长度是一样的 接下来将展示更多的RNN架构