高阶函数

高阶函数
映射
- map
- for-each
过滤
归档
排序
apply
编写高阶函数
- member-if 和 member
- 不规则曲线

高阶函数

高阶函数（Higher Order Function）是一种以 函数为参数的函数 。它们被用于映射、过滤、归档和排序表

高阶函数 提高了程序的模块性 。编写对各种情况都适用的高阶函数与为单一情况编写递归函数相比，可以使程序更具可读性。比如说，使用一个高阶函数来实现排序可以 使用不同的条件来排序 ，这就将排序条件和排序过程清楚地划分开来。函数sort具有两个参数，其一是一个待排序的表，其二是定序函数。下面展示了按照大小将一个整数表正序排序， <函数就是两数的定序函数：

(sort '(7883 9099 6729 2828 7754 4179 5340 2644 2958 2239) <)
;; (2239 2644 2828 2958 4179 5340 6729 7754 7883 9099)

按照每个数末两位的大小排序可以按下面的方式实现：

(sort '(7883 9099 6729 2828 7754 4179 5340 2644 2958 2239) 
      (lambda (x y) (< (modulo x 100) (modulo y 100))))
;; (2828 6729 2239 5340 2644 7754 2958 4179 7883 9099)

    正如这里所演示的，像 快速排序 、 归并排序 等排序过程，如果把 定序函数 完全分离开来 提高了代码的复用性

由于 Scheme 并不区别过程和其它的数据结构 ，因此可以通过 将函数当作参数传递 ，轻松的定义自己的高阶函数

    实际上，Scheme中预定义函数的本质就是高阶函数

    因为Scheme并没有定义 块结构 的语法，因此使用 lambda表达式 作为一个块

映射

映射是将 同样的行为应用于表所有元素 的过程。R5RS定义了两个映射过程：

map 过程：返回转化后的表
for-each 过程：注重副作用

map

map 过程的格式如下：

(map procedure list1 list2 ...)

procedure ：与某个过程或 lambda表达式相绑定的符号
作为参数的表的个数视 procedure需要的参数而定

; Adding each item of '(1 2 3) and '(4 5 6).
(map + '(1 2 3) '(4 5 6)) ; (5 7 9) 

; Squaring each item of '(1 2 3)
(map (lambda (x) (* x x)) '(1 2 3)) ; (1 4 9)

for-each

for-each的格式与map一致。但for-each并不返回一个具体的值，只是 用于副作用

(define sum 0)
(for-each (lambda (x) (set! sum (+ sum x))) '(1 2 3 4))
sum ;  10

过滤

    过滤函数并没有在 R5RS 中定义

    但MIT-Scheme实现提供了 keep-matching-items 和 delete-matching-item 两个函数

(keep-matching-items '(1 2 -3 -4 5) positive?) ;  (1 2 5)

归档

    尽管在R5RS中没有定义归档函数

    但MIT-Scheme提供了 reduce 等函数

(reduce + 0 '(1 2 3 4))                 ;  10
(reduce + 0 '(1 2))                     ;  3
(reduce + 0 '(1))                       ;  1
(reduce + 0 '())                        ;  0
(reduce + 0 '(foo))                     ;  foo
(reduce list '() '(1 2 3 4))            ;  (4 (3 (2 1)))

排序

    尽管R5RS中没有定义 排序 函数

    但MIT-Scheme提供了 sort（实为merge-sort实现）和 quick-sort 函数

(sort '(3 5 1 4 -1) <) ; (-1 1 3 4 5)

apply

apply 函数：将一个过程应用于一个_表_ 。此函数具有任意多个参数：

首参数：应该是一个过程
末参数：应该是一个表

      将表展开，作为过程的参数

    虽然乍看之下不然，但这个函数的确非常方便

(apply max '(1 3 2))      ;  3
(apply + 1 2 '(3 4 5))    ;  15
(apply - 100 '(5 12 17))  ;  66

编写高阶函数

自己编写高阶函数非常容易

member-if 和 member

member-if 函数：

使用一个谓词和一个表作为参数
返回一个子表，该子表的car部分即是 原列表中首个满足该谓词的元素

member-if函数可以像下面这样定义：

(define (member-if proc ls)
  (cond
   ((null? ls) #f)
   ((proc (car ls)) ls)
   (else (member-if proc (cdr ls)))))

(member-if positive? '(0 -1 -2 3 5 -7)) ; (3 5 -7)

member 函数 检查特定元素是否在表中 ，函数需要三个参数：

用于比较的函数
特定项
待查找表

(define (member proc obj ls)
  (cond
   ((null? ls) #f)
   ((proc obj (car ls)) ls)
   (else (member proc obj (cdr ls)))))

(member string=? "hello" '("hi" "guys" "bye" "hello" "see you")) ; ("hello" "see you")

不规则曲线

生成像 C曲线、龙曲线等不规则曲线可以通过在 两个点中插入一个点 来实现

先定义一系列的辅助函数：

;;; 平面直角坐标系上的点通过序对来表示，其中car部分和cdr部分分别代表
;;; x坐标和y坐标。
;;; 函数_x和_y用来取得坐标，point用来建立一个点
(define _x car)
(define _y cdr)
(define point cons)

;;; 接受两个表作为参数，将第一个表反转后与第二个表连接起来。
(define (rappend ls0 ls1)
  (let loop((ls0 ls0) (ls1 ls1))
    (if (null? ls0)
        ls1
        (loop (cdr ls0) (cons (car ls0) ls1)))))

;; (rappend '(1 2 3) '(4 5 6)) -> (3 2 1 4 5 6)

;;; (devide p1 p2 r)
;;; dividing p1 and p2 internally by the ratio r
(define (divide p1 p2 r)
  (point (+ (* r (_x p1)) (* (- 1.0 r) (_x p2)))
         (+ (* r (_y p1)) (* (- 1.0 r) (_y p2)))))

;;; 将点输出至文件。将一系列点points按一行一个点得格式输出至fout代表的文件
(define (print-curve points fout)
  (with-output-to-file fout
    (lambda ()
      (for-each
       (lambda (p)
         (display (_x p))
         (display " ")
         (display (_y p))
         (newline))
       points))))

frac 函数：

;;; (fractal proc n points fout)
;;; 创建分型图形的高阶函数。其中，proc是定位函数，n是重复次数
;;; points是初始点构成的表，fout是输出文件的文件名
(define (fractal proc n points fout)
  (let loop((i 0) (points points)) ;; loop对数据表做n次插入
    (if (= n i)
        (print-curve points fout)
        (loop
         (1+ i)
         (let iter ((points points) (acc '())) ;;  iter 调用 proc 函数把点加入一个列表
           (if (null? (cdr points)) 
               (reverse! (cons (car points) acc))
               (iter
                (cdr points)
                (rappend (proc (first points) (second points)) acc))))))) ;; proc 函数有2个参数，两个点，返回第一个点和插入点的列表
  'done)

定义各种曲线：

;;; c curve
(define (c-curve p1 p2) 
  (let ((p3 (divide p1 p2 0.5)))
    (list
     p1
     (point (+ (_x p3) (- (_y p3) (_y p2)))
            (+ (_y p3) (- (_x p2) (_x p3)))))))

;;; dragon curve
(define dragon-curve 
  (let ((n 0))
    (lambda (p1 p2)
      (let ((op (if (even? n) + -))
            (p3 (divide  p1 p2 0.5)))
        (set! n (1+ n))
        (list
         p1
         (point (op (_x p3) (- (_y p3) (_y p2)))
                (op (_y p3) (- (_x p2) (_x p3)))))))))

;;; koch curve
(define (koch p1 p2)
  (let ((p3 (divide p1 p2 2/3))
        (p4 (divide p1 p2 1/3))
        (p5 (divide p1 p2 0.5))
        (c  (/ (sqrt 3) 2)))
    (list
     p1
     p3
     (point (- (_x p5) (* c (- (_y p4) (_y p3))))
            (+ (_y p5) (* c (- (_x p4) (_x p3)))))
     p4)))

测试：

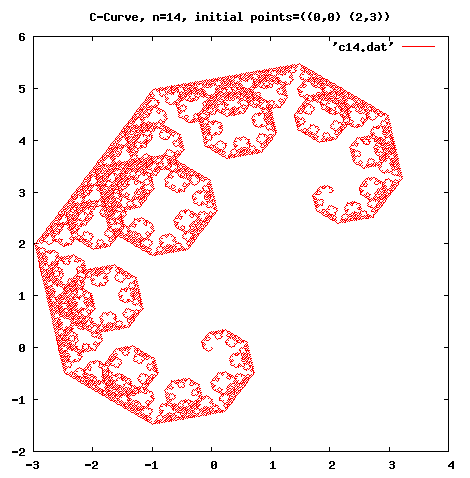
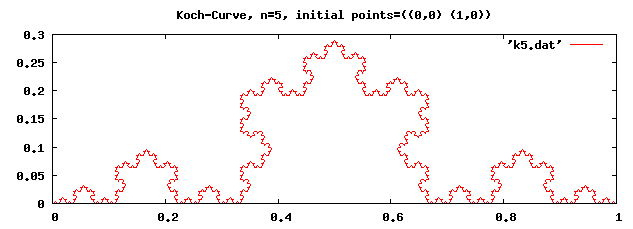
(compile-file "frac.scm")
(load "frac")

;; C-Curve
(fractal c-curve 14 '((0 . 0) (2 . 3)) "c14.dat")

;; Dragon-Curve
(fractal dragon-curve 14 '((0 . 0) (1 . 0)) "d14.dat")

;; Koch-Curve
(fractal koch 5 '((0 . 0) (1 . 0)) "k5.dat")